Cool Problem of the Month - 2

Yapping

I recently have had the hobby of going through past AMC and AIME problems and trying to see if I could think of any goofy solution that’s not on the list of solutions on the AoPS wiki.

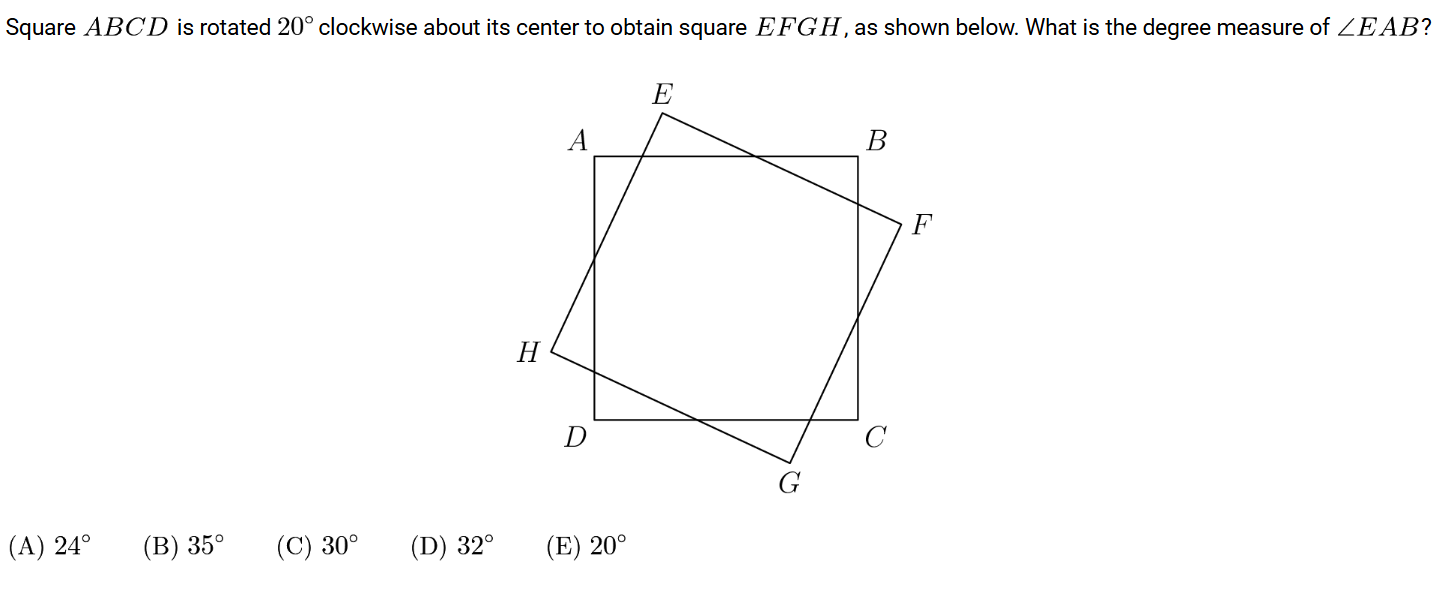
For one problem in particular, 2023 AMC 10B #7 (yeah, it’s still in the single digits), I found a diabolical solution that no one would have wanted to waste their brain cells to completely formulate. It is super easy to do just using 4th grade knowledge of geometry, but when I see rotations in geometry, I immediately think of complex bashing.

The problem with answer choices

I actually wrote this solution on AoPS wiki last month, but this crazy backstory deserves its own post for Cool Problem of the Month, and November was already taken. See the solution I wrote here.

I tried to reword or explain some of the solution a bit more in depth, so you can rest assured that I didn’t just plainly plagiarize myself.

The complex and trig bashing itself isn’t even bad. If the problem was at least in the double digits, it would likely have been perfectly acceptable to complex bash and then trig bash. However, for a question #7, I’m probably going to be socially ostracized for having done so, especially when a nine year old obsessed with Tung Tung Tung Sahur can beat you to it.

Without further ado, here is the solution.

Solution

Let the center of the square be the origin of the complex plane. Since we only care about angles, and not sides, we can assume WLOG that \(A\) is at the point \(-1+i\). To rotate a complex number clockwise by an angle \(\theta\), just multiply the number by \(e^{-i \theta}\), so then we end up decreasing the argument (angle measured counterclockwise from the x-axis) by \(\theta\) while preserving the magnitude. In this case \(\theta = 20^{\circ}\).

So, the point \(A'\) is at \((-1+i)(e^{-i 20^{\circ}}) = (-1+i)(\cos( - 20^{\circ}) + i \sin( - 20^{\circ}))\) from Euler’s formula (the exponential form is just my shorthand way of remembering how to rotate complex numbers, but you could just go straight to polar form). Since cosine is an even function and sine is odd, this is the same as \((-1+i)(\cos(20^{\circ}) - i \sin(20^{\circ}))\). This expands to \((-\cos(20^{\circ}) + \sin(20^{\circ})) + i(\cos(20^{\circ}) + \sin(20^{\circ}))\).

The angle we want to find is just the direction of the vector from \(A\) to \(A'\). So, this is just \(\arctan(\frac{\Delta \Im}{\Delta \Re})\). \(\Delta \Im = \cos(20^{\circ}) + \sin(20^{\circ}) - 1\), while \(\Delta \Re = -\cos(20^{\circ}) + \sin(20^{\circ}) + 1\). Essentially, the problem is just boiled down to finding out how to trig bash \(\arctan(\frac{\cos(20^{\circ}) + \sin(20^{\circ}) - 1}{-\cos(20^{\circ}) + \sin(20^{\circ}) + 1})\).

The is an identity that \(\cos(A)+\sin(A)=\sqrt{2}\sin(A+45^{\circ})\) and \(\cos(A)-\sin(A)=\sqrt{2}\cos(A+45^{\circ})\). I’ll leave it as an exercise to the reader to verify that. So, if we use this as well as the fact that \(\sin(90^\circ - x) = \cos(x)\), the fraction simplifies to \(- \frac{\sqrt{2} \cos(25^\circ)-1}{\sqrt{2} \sin(25^\circ)-1}\). Substituting \(\sqrt{2}=\frac{1}{\cos(45^\circ)}\), this simplifies to \(- \frac{\cos(25^\circ)-\cos(45^\circ)}{\sin(25^\circ)-\cos(45^\circ)} = - \frac{\cos(25^\circ)-\cos(45^\circ)}{\sin(25^\circ)-\sin(45^\circ)}\).

Finally, there is an identity that \(\cos(A)-\cos(B)=-2\sin(\frac{A+B}{2})\sin(\frac{A-B}{2})\), and that \(\sin(A)-\sin(B)=2\cos(\frac{A+B}{2})\sin(\frac{A-B}{2})\). Again, verifying it is an exercise for the reader. So, we now have \(- \frac{2 \sin(35^\circ)\sin(10^\circ)}{-2 \cos(35^\circ)\cos(10^\circ)}\) = \(\tan(35^\circ)\), so \(\arctan(\tan(35^\circ)) = \boxed{35^\circ}\), or option \(B\).